临近考研、面试，抽了几个平时不太会写的排序算法重新温习了一下，下面做个总结，亦或者说用一句话概括一下简略思想吧。

插入排序

假设前$i-1$个元素已经有序，那么很容易通过$O(n)$的算法应该插入的位置，使得前i个元素有序，所以复杂度为：$O(n^2)$

冒泡排序

假设前$i$个元素已经是已知序列中的前$i$小元素，并且已经有序，那么将后面$n-i$个元素中的最小值(第$i+1$小元素)通过交换置换到$i+1$的位置即可。

堆排序

前置知识：

• 首先要知道堆其实是一种二叉树的树形数据结构，在保证一个节点的权值比两个孩子节点都要大(小)的情况下，成为大(小)根堆。
• 可以利用完全二叉树的性质，直接用数组来模拟树形结构，那么对于编号$[0,n-1]$的数组来说，$i$的左孩子即为:$i\times 2+1$,右孩子即为$i\times 2+2$,对于编号$[1,n]$的数组来说，左孩子即为:$i\times 2$,右孩子即为$i\times 2+1$，父节点编号也可以自行推出。

基础思路：

初始化堆

• 此时可以建立与树形dp相关的思路，保证子树都满足节点值大于左右孩子值。
• 所以此时由下向上进行树形dp，每次对于一个新来的元素$x$，都可以找到$x$会被替换到什么位置。
• 从最后一个非叶子节点开始，每次都将这个节点插入到其子树的某个位置中，因为满足$dp$的性质:子树都满足大(小)根堆的性质，那么一旦发现这个数比左右孩子都大(小)，停止就可以了。

堆调整(AdjustHeap)

堆调整就是初始化堆时，对于第x个数，应该插入到什么位置。
复杂度:$O(logn)$

堆排序

1. 首先初始化堆，利用堆调整函数
2. 初始化堆完成后，最大(小)值应该是根元素，将此时根元素和最后一个叶子节点元素互换位置，将剩下的$n-1$个元素组成一个新的堆，由于这个新的堆保留着初始化堆的性质，交换第一个与第$n$个元素之后，就相当于根元素发生了变化需要重新进行一次堆调整$(AdjustHeap)$.
3. 执行$n-1$次之后，数组就有序了

快速排序

选择一个基值，分别需要一个左、右指针，将左边大于基值的都放在基值右边，将右边大于基值的都放在基值左边。这样一来，基值的位置就确定了，由基值继续进行分治，所以复杂度是$O(nlogn)$，最坏复杂度$O(n^2)\to$取决于基值的选择。

基数排序

这个排序时间上应该是最优的，如果基数选择合理。一般取$lo{g}_{10}(a_i)$，所以复杂度是$nlo{g}_{10}(a_i)$。

思路是基于桶排的，首先先从个位数开始进行排序，然后十位数、 百位数$\dots$最高位数，这样只需要借助一个外来的辅助空间即可完成排序。

因为需要借助辅助空间，所以空间复杂度和时间复杂度均为$o(n\ast k)$

归并排序

分治思想即可，假设$[l,mid]$与$[mid+1,r]$均有序，所以可以借助额外的辅助空间进行两个区间的有序链表合并，所以时空复杂度均为$O(nlogn)$

Code:

/*** keep hungry and calm CoolGuang!  ***/
//#pragma GCC optimize(3)
#include <bits/stdc++.h>
#define debug(x) cout<<#x<<":"<<x<<endl;
#define dl(x) printf("%lld\n",x);
#define di(x) printf("%d\n",x);
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
const ll INF= 1e18+7;
const int maxn = 1e6+7;
const int mod= 1e9+7;
const double eps = 1e-9;
const double PI = acos(-1);
template<typename T>inline void read(T &a){char c=getchar();T x=0,f=1;while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}a=f*x;}
ll m,p;

class test{
	public :
		test(int _N){
			n = _N;
			for(int i=1;i<=n;i++) s[i] = i;
			printf("test constructed\n");
		}
		~test(){
			printf("test destroyed\n");
		}
		void write(){
			for(int k=1;k<=n;k++)
				printf("%d ",s[k]);
			printf("\n");
		}
		void SrandBack(){random_shuffle(s+1,s+1+n);}
		void InsertSort(){
			for(int i=1;i<=n;i++){//前i-1个已经有序
				int k = i-1,t = s[i];
				while(k>=1&&s[k]>t){
					s[k+1] = s[k];
					k--;
				}
				s[k+1] = t;
			}
		}
		void BubbleSort(){
			for(int i=1;i<=n;i++){
				for(int k=n-1;k>=i;k--){
					if(s[k+1]<s[k]) swap(s[k],s[k+1]);
				}
			}
		}

		void AdjustHeap(int len,int pos){
			int tmp = s[pos];
			for(int i=2*pos;i<=len;i=2*i){
				if(i+1<=len && s[i+1]>s[i]) i++;
				if(s[i]>tmp){
					s[pos] = s[i];
					pos = i;
				}else break;
			}
			s[pos] = tmp;
		}
		void HeapSort(){
			///Restore Heap
			for(int i=n/2;i>=1;i--) AdjustHeap(n,i);
			///HeapSort
			for(int i=n;i>=2;i--){
				swap(s[i],s[1]);
				AdjustHeap(i-1,1);
			}
		}
		void work(int L,int R){
			if(L>=R) return;
			int tmp = s[(L+R)/2];
			int l = L,r = R;
			while(l<r){
				while(l<r && s[r]>tmp) r--;
				while(l<r && s[l]<tmp) l++;
				if(l<=r){
					swap(s[l],s[r]);
					l++;
					r--;
				}
			}
			work(l,R);
			work(L,r);
		}
		void QuickSort(){work(1,n);}	
		void Merge(int l,int r){
			if(l>=r) return;
			int mid = (l+r)/2;
			Merge(l,mid);
			Merge(mid+1,r);
			int L = l,R = mid+1;
			int cnt = 0;
			while(L<=mid && R<=r){
				if(s[L]  <= s[R]) cp[++cnt] = s[L++];
				else cp[++cnt] = s[R++];
			}
			if(L<=mid) for(int k=L;k<=mid;k++) cp[++cnt] = s[k];
			if(R<=r) for(int k=R;k<=r;k++) cp[++cnt] = s[k];
			for(int k=1;k<=cnt;k++) s[l+k-1] = cp[k];
		}
		void MergeSort(){Merge(1,n);}
		void RadixSort(){
			int maxlen = 0,mx = 0;
			for(int k=1;k<=n;k++) mx = max(mx,s[k]);
			while(mx){maxlen++;mx/=10;}
			int base = 1;
			while(maxlen--){
				int cnt = 0;
				for(int k=0;k<=9;k++) c[k][0] = 0;
				for(int k=1;k<=n;k++){
					int idx =(s[k]/base)%10;
					c[idx][++c[idx][0]] = s[k];
				}
				for(int k=0;k<=9;k++){
					for(int i=1;i<=c[k][0];i++)
						s[++cnt] = c[k][i];
				}
				base *= 10;
			}
		}
	private:
		int s[1005],cp[1005],n;
		int c[1005][10];//Radix
};
int main(){
  auto p = make_shared<test>(10);
  printf("-------InsertSort--------\n");
  p->SrandBack();
	p->write();
	p->InsertSort();
	p->write();
	printf("-------BubbleSort--------\n");
	p->SrandBack();
	p->write();
	p->BubbleSort();
	p->write();
	printf("-------HeapSort--------\n");
	p->SrandBack();
	p->write();
	p->HeapSort();
	p->write();
	printf("-------QuickSort--------\n");
	p->SrandBack();
	p->write();
	p->QuickSort();
	p->write();
	printf("-------MergeSort--------\n");
	p->SrandBack();
	p->write();
	p->MergeSort();
	p->write();
	printf("-------RadixSort--------\n");
	p->SrandBack();
	p->write();
	p->RadixSort();
	p->write();
  return 0;

}

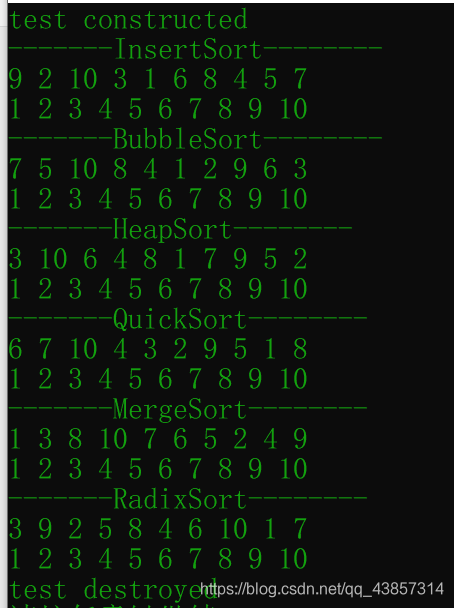
运行截图：

原文链接:https://blog.csdn.net/qq_43857314/article/details/117666594