前面有同学想做中国象棋的游戏，丁老师夸口一天能做完，结果被抓住了辫子，要在晚自习结束前，12小时内做完（不离开机房，不能上网）。用手机搜索一下，一般用最小最大策略搜索来弄。基于深度学习的程序，没有基础，一天定然是做不出来的，因此，我们先用搜索算法做一个能够玩的样本来。最终发现，效果还挺好，具有一定的棋力，尤其是残局。
代码详见
https://codechina.csdn.net/coloreaglestdio/qtcpp_demo/-/tree/master/chesspi
对奕过程可以参考
例子文件

1. 问题分析

中国象棋复杂的不是绘图和贴图，主要有三部分。

1. 规则控制。包括不同籽粒的走位、杀、将。仔细的控制走位，避免异常的违规走位。
2. 内存控制。在可控的内存下完成搜索树的构建。描述棋子状态的参数要尽可能的小，否则要不了3,4层，内存就耗尽了。
3. 决策算法。既要考虑自己的损失，也要考虑击杀对手。

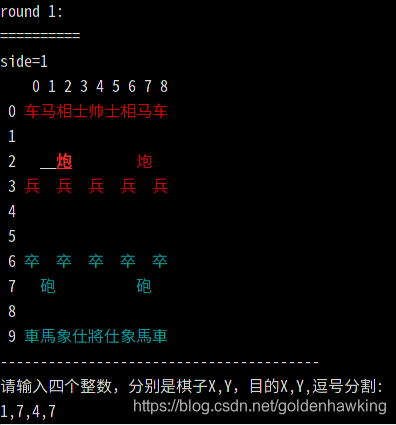
我们使用GNU C++ 64bit 在RaspberryPi4 8GB 版本的控制台Bash终端里实现一个字符界面的象棋程序，在12小时的工作量内完成开发（笔者用了9小时）。界面类似下图，通过输入横纵坐标来移动棋子。
注意笔者使用的树莓派有8GB内存，安装了64位的OS。在PC Windows下或者Linux下，本代码也建议用64位编译。

2. 棋盘构造与维护

2.1 棋盘状态

象棋棋子有32枚，使用一个32字节的坐标数组来描述每个棋子的位置。每个棋子一个字节，高4位为X，低四位为Y。这样尽可能的减少棋盘的体积。

其数据结构如下：

/**
	 * @brief coords 棋盘坐标，
	 * 每个字节一个棋子，X（高4比特）Y（低4比特），X1-9,Y1-10
	 * 顺序：0-15=红方0， 16-31=黑方1
	 * 0                         15 16                       31
	 * 帅士士相相马马车车炮炮兵兵兵兵兵  將仕仕象象馬馬車車砲砲卒卒卒卒卒
	 */
	unsigned char coords[32]{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};

同时，可以安排一个4字节的无符号整形，来表示每个棋子的生死。

	/*!
	 * \brief alive 存活标记，每个1比特.顺序：红方(0) 黑方(1)
	 * 0                        15 16                        31
	 * 帅士士相相马马车车炮炮兵兵兵兵兵  將仕仕象象馬馬車車砲砲卒卒卒卒卒
	 */
	unsigned int alive = 0;

这样安排后，一个树节点的大小相对来说要紧凑一些。

2.2 走位算法

走位算法给定初态、红黑方指示，得到当前状态的所有走法。这里要注意的是：

1. 走位算法红方与黑方的坐标不同。为了方便程序开发，我们采用翻转坐标的方法，只为红方编写走位逻辑。这样的好处是要判断的环节少，逻辑单一，便于调试。
2. 将碰头问题、马別腿等规则需要额外处理。

黑方在走位前，整体旋转棋盘，即可利用红方算法进行走位。具体代码详见Git版本库。

std::vector<chess_node>  expand_node(const chess_node & r_root, const int side);

性能：由于C++20的容器支持右值引用，作为参数返回是木有问题的。

2.3 打印棋盘

打印棋盘要用到不同的色彩，需要Bash \033转义。
使用转义符，可以控制Bash的色彩。

if (map_coords[y][x]>0 && map_coords[y][x]<=16)
	printf("\33[1m\033[31m%s\033[0m",pstr[map_coords[y][x]-1]);
else if (map_coords[y][x]>16)
	printf("\33[1m\033[36m%s\033[0m",pstr[map_coords[y][x]-1]);
else
	printf ("  ");

需要注意的是，我的Bash是黑色的，如果不是黑色的，可以参考这里调整色彩。

3. 搜索策略

象棋最复杂的莫过于搜索策略。笔者花在这个上面的时间应该更多，但是太累了，准备把这一块留给同学们来完善了。目前的算法，还是比较基础的，我因为两次坐标输入失误，输了几盘。由于搜索深度随着籽粒减少而更深，在中残局上表现的非常鬼，尤其是残局，不小心是会翻车的。

算法目前使用广度优先建树、逆向遍历加权的方法来决定最佳的路径。主要考虑有：

1. 不同的棋子有不同的基础价值。
2. 棋子的实际价值，还与状态有关。过了河的卒子价值高，深入对手的马价值高，开局时的炮价值高，随着场上棋子的减少，马的价值渐渐高于炮。相士双全时的籽粒价值高于缺失时的籽粒价值，等等。

3.1 跳转代价

跳转代价是从父节点跳转到本节点造成的吃子损耗。

static const unsigned int table_cost[16] = {100000,150,150,150,150,150,150,500,500,150,150,100,100,100,100,100};
float jump_cost[2]{0,0};//跳转损失

jump_cost 分别记录红方、黑方的吃子代价。

3.2 OpenMP并行建树

建立树时，使用OpenMP进行加速。同时，使用哈希集合防止无谓的重复图案出现。

1. 需要注意OpenMP运行时，不能修改树本身，需要为每个线程设置缓存。
2. 一旦本轮创建完毕，使用std::move直接插入，而不要使用std::copy。
3. 哈希表要用临界区保护。

std::vector<chess_node> build_tree(const chess_node & root, const int side,const std::vector<chess_node> & history)
{
	std::vector<chess_node> tree;
	std::unordered_set <std::string> dict;
	//...
	size_t curr_i = 0;
	size_t max_nodes = 1024*1024*4;
	while (tree.size()<=max_nodes && curr_i<tree.size())
	{
		const size_t ts = tree.size();
		const int cores = omp_get_num_procs();
		std::vector<std::vector<chess_node> > vec_appends;
		for (int i=0;i<cores;++i)
			vec_appends.push_back(std::vector<chess_node>());
		std::atomic<int> new_appends (0);
#pragma omp parallel for
		for (int i=curr_i;i<ts;++i)
		{
			if (new_appends + ts >=max_nodes)
				continue;
			const unsigned char clock = tree[i].depth;
			const int tid = omp_get_thread_num();
			if ((tree[i].alive & 0x00010001)==0x00010001)
			{
				const int curr_side = (side + clock) % 2;
				std::vector<chess_node> next_status =
						expand_node(tree[i],curr_side);

				const size_t sz = next_status.size();
				for (size_t j=0;j<sz;++j)
				{
					std::string ha = node2hash(next_status[j].coords,next_status[j].alive);
					bool needI = false;
#pragma omp critical
					{
						if (dict.find(ha)==dict.end())
						{
							needI = true;
							dict.insert(ha);
						}
					}
					if (needI)
					{
						//...
						vec_appends[tid].push_back(next_status[j]);
						//...
					}
				}
			}
		}
		for (int i=0;i<cores;++i)
		{
			if (vec_appends[i].size())
				std::move(vec_appends[i].begin(),vec_appends[i].end(),std::back_inserter(tree));
		}
		curr_i += (ts - curr_i);
	}
	//...
	return tree;
}

3.3 跳转概率与代价传递

对某个节点来说，其具备红黑属性。谁都会选择对自己最有利的局面走。因此，当前节点的跳转概率就是对手的代价/我的代价。

当遍历时，从最底层节点开始，往根部遍历。各个节点的本级代价（jump_cost)会和本级跳转概率加权后累加给父节点。这样，当遍历完成后，首层孩子中最大概率的那个节点就是最优节点。

1. 调整跳转概率的生成，可以控制对手是保守型，还是进攻型。
2. 调整代价传递，会影响到AI对局面的估计。

size_t judge_tree(std::vector<chess_node> & tree)
{
	const size_t total_nodes = tree.size();
	if (total_nodes<2)
		return 0;
	int side = tree[0].side;
	size_t i = total_nodes - 1;
	while (i > 0)
	{
		if (tree[i].side==0)
		{
			float ratio = sqrt((tree[i].jump_cost[1]+1) / (tree[i].jump_cost[0]+1)/ (tree[i].jump_cost[0]+1));
			tree[i].weight = ratio;
		}
		else
		{
			float ratio = sqrt((tree[i].jump_cost[0]+1) / (tree[i].jump_cost[1]+1)/ (tree[i].jump_cost[1]+1));
			tree[i].weight = ratio;
		}
		size_t parent = tree[i].parent;
		tree[parent].jump_cost[0] += tree[i].jump_cost[0] * tree[i].weight/tree[i].depth/tree[i].depth;
		tree[parent].jump_cost[1] += tree[i].jump_cost[1] * tree[i].weight/tree[i].depth/tree[i].depth;
		--i;
	}
    /...
}

4. 回合举例

可以看看下面这个回合，电脑执黑，3,1处的车占据了地形，结果它把炮从2,0转到2,1，准备抽车上3,5吃掉我的兵。

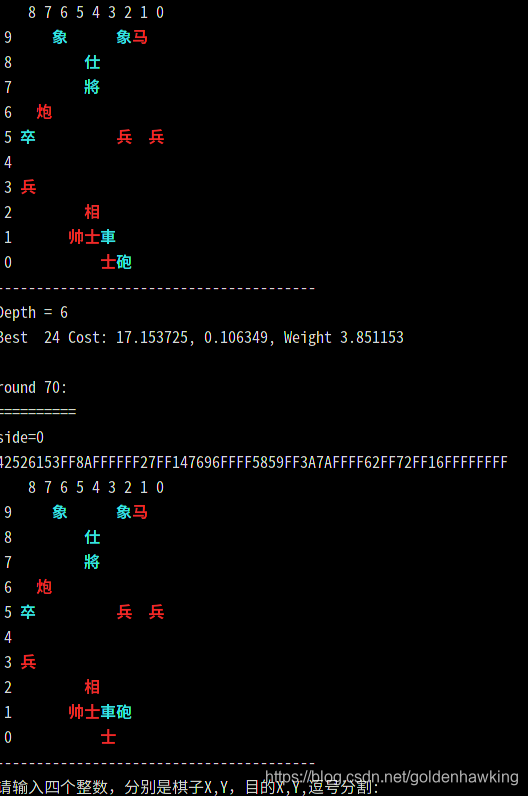
我只顾着将军，没有注意到，结果：

说明这样简单的算法还是有少许“AI”的。

5 后续

请感兴趣的同学改进算法，增强在开局时的智能性。

原文链接:https://blog.csdn.net/goldenhawking/article/details/117534567