机器学习—K-means聚类、密度聚类、层次聚类理论与实战-php黑洞网

本站消息

站长简介/公众号

出租广告位,需要合作请联系站长

搜嘎皮卡

2111

文章

882244

访问

+关注

分类

暂无分类

日期归档

2024-11(1)

机器学习—K-means聚类、密度聚类、层次聚类理论与实战

发布于2021-05-30 18:40 阅读(773) 评论(0) 点赞(20) 收藏(3)

文章目录

引言

聚类是机器学习算法中“新算法”出现最多、最快的领域。一个重要的原因是聚类不存在客观标准。下面我们分别介绍K-means聚类、DBSCAN算法（密度聚类）、AgglomerativeClustering算法（层次聚类）。

一、K-means聚类

1.算法原理

在这里插入图片描述

2.算法参数、属性、方法介绍

sklearn.cluster.KMeans

class sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001, 
precompute_distances='deprecated', verbose=0, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto')

参数介绍：

n_clusters:一个整数,指定分类簇的数量。
init:一个字符串，指定初始均值向量的策略。可以为如下：
- ‘k-means++’:该初始化策略选择的初始均值向量相互之间都距离较远，它的效果较好(这个策略一定程度上可以解决K均值算法收敛依赖初始化的均值的问题)
- ‘random’:从数据集中随机选择K个样本作为初始均值向量。
- 或者提供一个数组，数组的形状为(n_clusters.n_features)，该数组作为初始均值向量。
n_init:一个整数，指定了k均值算法运行的次数。每一次都会选择一组不同的初始化均值向量，最终算法会选择最佳的分类簇来作为最终的结果。
max_iter:一个整数，指定了单轮k均值算法中，最大的迭代次数。算法总的最大迭代次数为max_iter * n_init。
precompute_distances:可以为布尔值或者字符串’auto’。该参数指定是否提前计算好样本之间的距离（如果提前计算距离,则需要更多的内存,但是算法会运行得更快)。
- auto’:如果n_samples*n_clusters > 12 million，则不提前计算;
- True:总是提前计算;
- False:总是不提前计算。
tol:一个浮点数,指定了算法收敛的阈值。
n_jobs:一个正数。指定任务并形时指定的CPU数量。如果为-1则使用所有可用的CPU。
verbose:一个整数。如果为0，则不输出日志信息;如果为1，则每隔一段时间打印一次日志信息;如果大于1，则打印日志信息更频繁。
random_state:一个整数或者一个RandomState实例，或者None。
- 如果为整数,则它指定了随机数生成器的种子。
- 如果为RandomState实例，则指定了随机数生成器。
- 如果为None，则使用默认的随机数生成器。
copy_x:布尔值，主要用于precompute_distances=True的情况。
- 如果为True，则预计算距离的时候，并不修改原始数据。
- 如果为False，则预计算距离的时候，会修改原始数据用于节省内存;然后当算法结束的时候，会将原始数据返还。但是可能会因为浮点数的表示，会有一些精度误差。

属性介绍：

cluster_centers_:给出分类簇的均值向量。
labels_:给出了每个样本所属的簇的标记。
inertia_:给出了每个样本距离它们各自最近的簇中心的距离之和。
n_iter_ : 迭代次数

方法介绍：

fit(XL,y]):训练模型。
fit_predict(X[，y]):训练模型并预测每个样本所属的簇。它等价于先调用fit方法,后调用predict方法。
predict(X):预测样本所属的簇。
score(X[，y]):给出了样本距离个簇中心的偏移量的相反数。

3.算法实战

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score


# make_blobs函数产生的是分隔的高斯分布的聚类簇
def create_data(centers, num=100, std=0.7):
    X, labels_true = make_blobs(n_samples=num, centers=centers, cluster_std=std)
    return X, labels_true


# 观察生成点
def plot_data(*data):
    X, labels_true = data
    labels = np.unique(labels_true)
    fig, ax = plt.subplots()
    colors = 'rgbyckm'
    for i, label in enumerate(labels):
        position = labels_true == label
        # 散点图
        ax.scatter(X[position, 0], X[position, 1], label="cluster %d" % label, color=colors[i % len(colors)])
    # 图例位置
    ax.legend(loc='best')
    ax.set_xlabel("X_0")
    ax.set_ylabel("X_1")
    ax.set_title('data')
    plt.show()


# 考察簇的数量
def test_Kmeans(*data):
    X, label_true = data
    nums = range(1, 20)
    # ARI指数
    ARIS = []
    Distances = []
    for num in nums:
        cls = cluster.KMeans(n_clusters=num, init='k-means++')
        cls.fit(X)
        predicted_labels = cls.predict(X)
        # ARI指标
        ARIS.append(adjusted_rand_score(label_true, predicted_labels))
        # 距离之和
        Distances.append(cls.inertia_)
    return nums, ARIS, Distances


# 寻找最佳聚类中心
def plot_kmeans(*data):
    fig, ax = plt.subplots(1, 2, figsize=(8, 8))
    ax[0].plot(nums, ARIS, marker="+")
    ax[0].set_xlabel("n_clusters")
    ax[0].set_ylabel("ARI")
    ax[1].plot(nums, Distances, marker="o")
    ax[1].set_xlabel("n_cluster")
    ax[1].set_ylabel("Distances")
    fig.suptitle("KMeans")
    plt.show()


if __name__ == '__main__':
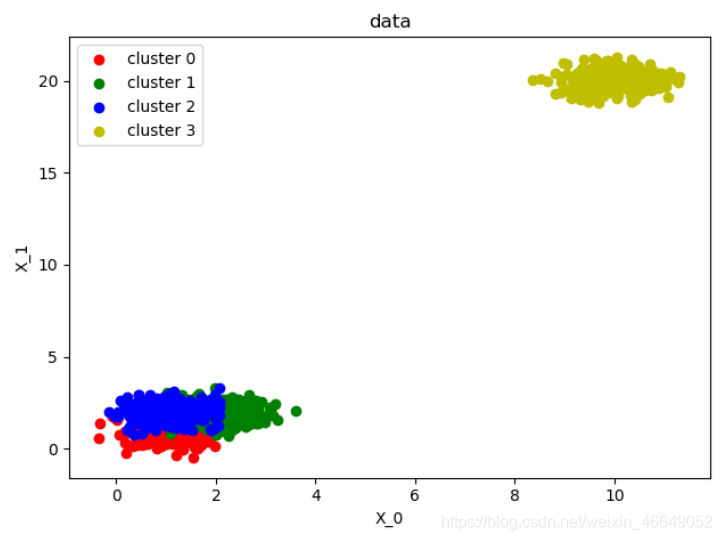
    centers = np.asarray([[1, 1], [2, 2], [1, 2], [10, 20]])
    # 构造数据
    X, labels_true = create_data(centers, num=1000, std=0.5)
    # 观察生成点
    plot_data(X, labels_true)
    nums, ARIS, Distances = test_Kmeans(X, labels_true)
    plot_kmeans(nums, ARIS, Distances)

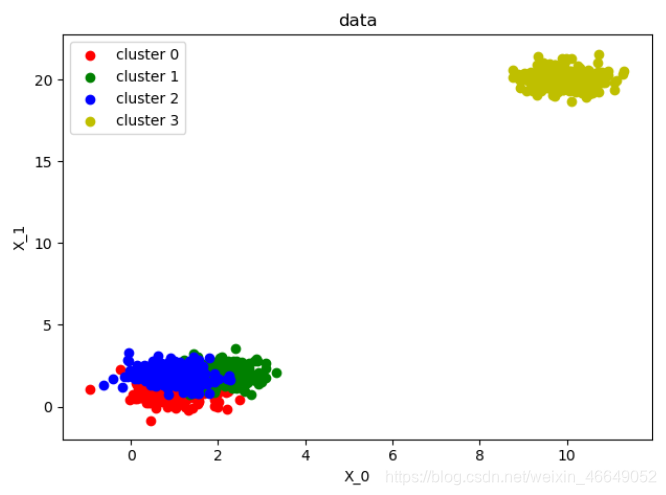
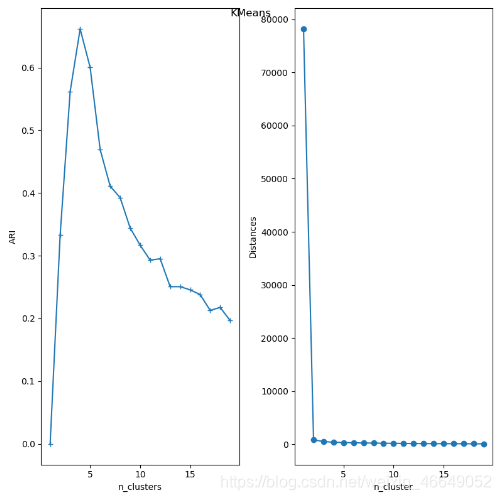
在这里插入图片描述

在这里插入图片描述
根据ARI指标发现，n_clusters=4时，ARI最大。

二、密度聚类—DBSCAN

1.算法原理

密度聚类假设聚类结构能够通过样本分布的紧密程度来确定。它通过一组邻域参数 $(\epsilon,MinPts)$ 来描述样本分布的紧密程度。
在这里插入图片描述

一些属性定义如下：

2. 算法参数、属性、方法介绍

class sklearn.cluster.DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean', metric_params=None, algorithm='auto',
 leaf_size=30, p=None, n_jobs=None)

参数介绍：

eps: $\epsilon$ 参数，用于确定邻域大小。
min_samples: MinPts参数，用于判断核心对象。
metric:一个字符串或者可调用对象，用于计算距离。如果是字符串，则必须是在metrics.pairwise.calculate_distance中指定。
algorithm:一个字符串，用于计算两点间距离并找出最近邻的点
- ‘auto’:由算法自动选取合适的算法。
- ‘ball_tree’:用ball树来搜索。
- 'kd_tree ':用kd树来搜索。
- ‘brute’:暴力搜索。
leaf_size:一个整数，用于指定当algorithm=ball_tree或者kd_tree时，树的叶节点大小。该参数会影响构建树、搜索最近邻的速度，同时影响存储树的内存。

属性介绍：

core_sample_indices_:核心样本在原始训练集中的位置。
components_:核心样本的一份副本。
labels_:每个样本所属的簇标记。对于噪声样本，其簇标记为-1副本。

方法介绍：

fit(X[，y，sample_weight]):训练模型。
fit_predict(X[， y, sample_weight]):训练模型并预测每个样本所属的簇标记。

3.算法实战

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score


# make_blobs函数产生的是分隔的高斯分布的聚类簇
def create_data(centers, num=100, std=0.7):
    X, labels_true = make_blobs(n_samples=num, centers=centers, cluster_std=std)
    return X, labels_true


# 观察生成点
def plot_data(*data):
    X, labels_true = data
    labels = np.unique(labels_true)
    fig, ax = plt.subplots()
    colors = 'rgbyckm'
    for i, label in enumerate(labels):
        position = labels_true == label
        # 散点图
        ax.scatter(X[position, 0], X[position, 1], label="cluster %d" % label, color=colors[i % len(colors)])
    # 图例位置
    ax.legend(loc='best')
    ax.set_xlabel("X_0")
    ax.set_ylabel("X_1")
    ax.set_title('data')
    plt.show()


# 考察eps-邻域大小
def test_DBSCAN(*data):
    X, label_true = data
    epsilons = np.logspace(-1, 1.5)
    # ARI指数
    ARIS = []
    Core_Nums = []
    for epsilon in epsilons:
        cls = cluster.DBSCAN(eps=epsilon)
        cls.fit(X)
        predicted_labels = cls.fit_predict(X)
        # ARI指标
        ARIS.append(adjusted_rand_score(label_true, predicted_labels))
        # 核心样本的数量
        Core_Nums.append(len(cls.core_sample_indices_))
    return epsilons, ARIS, Core_Nums


# 寻找最佳聚类中心
def plot_kmeans(*data):
    fig, ax = plt.subplots(1, 2, figsize=(8, 8))
    ax[0].plot(epsilons, ARIS, marker="+")
    ax[0].set_xlabel(r"$\epsilon$")
    ax[0].set_ylabel("ARI")
    ax[1].plot(epsilons, Core_Nums, marker="o")
    ax[1].set_xlabel(r"$\epsilon$")
    ax[1].set_ylabel("Core_Nums")
    fig.suptitle("DBSCAN")
    plt.show()


if __name__ == '__main__':
    centers = np.asarray([[1, 1], [2, 2], [1, 2], [10, 20]])
    # 构造数据
    X, labels_true = create_data(centers, num=1000, std=0.5)
    # 观察生成点
    plot_data(X, labels_true)
    epsilons, ARIS, Core_Nums = test_DBSCAN(X, labels_true)
    plot_kmeans(epsilons, ARIS, Core_Nums)

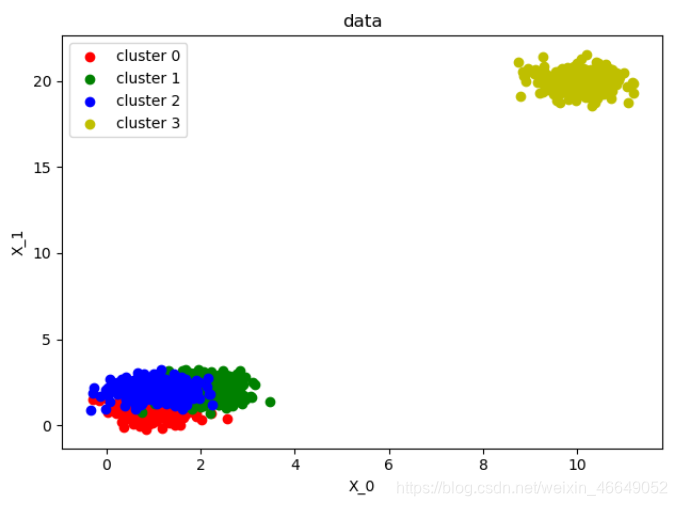
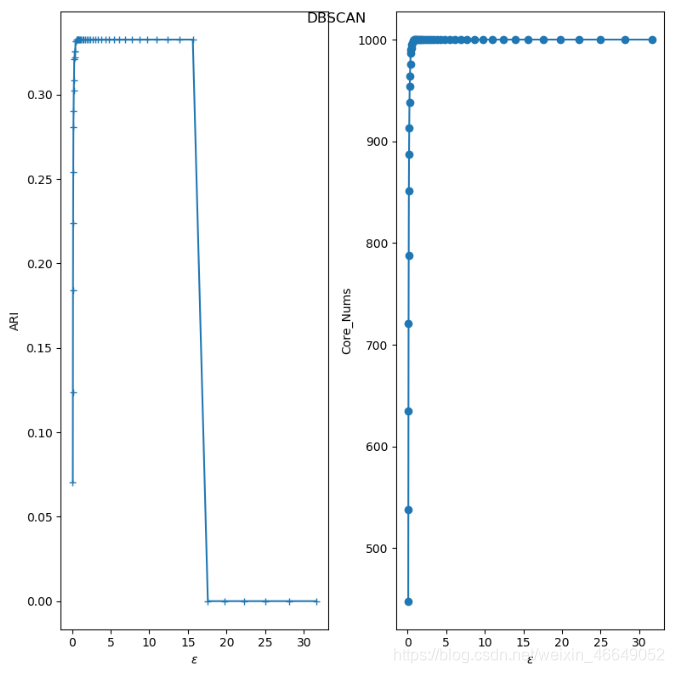
在这里插入图片描述

可以看到ARI指数随着 $\epsilon$ 的增长,先上升后保持平稳，最后断崖式下降。断崖式下降是因为我们产生的训练样本的间距比较小，最远的两个样本点之间的距离不超过30，当 $\epsilon$ 过大时，所有的点都在一个邻域中。
核心样本数量随着 $\epsilon$ 的增长而上升，这是因为随着 $\epsilon$ 的增长，样本点的邻域在扩展，则样本点邻域内的样本会更多，这就产生了更多满足条件的核心样本点。但是样本集中的样本数量有限，因此核心样本点的数量增长到一定数目后会趋于稳定。

三、层次聚类

1.算法原理

层次聚类算法可以在不同层上对数据集进行划分，形成树状的聚类结构。它的基本原理是：开始时将每个对象看成一个簇，然后这些簇根据某些准则（如距离最近)被一步步地合并，就这样不断地合并直到达到预设的聚类簇的个数。
在这里插入图片描述

2.算法参数、属性、方法介绍

class sklearn.cluster.AgglomerativeClustering(n_clusters=2, *, affinity='euclidean', memory=None, connectivity=None,
 compute_full_tree='auto', linkage='ward', distance_threshold=None, compute_distances=False)

参数介绍：

n_clusters: 一个整数,指定分类簇的数量。
connectivity:一个数组或者可调用对象或者为None，用于指定连接矩阵。它给出了每个样本的可连接样本。
affinity:一个字符串或者可调用对象，用于计算距离。可以为: ‘euclidean’，‘l1’,‘l2’, ‘manhattan’，’ cosine’,‘precomputed’，如果linkage=‘ward’，则’affinity必须是’euclidean’。
memory:用于缓存输出的结果，默认为不缓存。
compute_full_tree:通常当训练了n_clusters之后,训练过程就停止。但是如果compute.full_tree=True，则会继续训练从而生成一颗完整的树。
linkage:一个字符串，用于指定链接算法。
- ‘ward’:单链接single-linkage算法，采用 $d_{min}$
- ’ complete ':全链接complete-linkage算法，采用 $d_{max}$
- ‘average’:均链接average-linkage算法,采用 $d_{avg}$ 。
distance_threshold:超过这个链接距离阈值，簇将不会被合并。如果不是None，则n_clusters必须为None, compute_full_tree必须为True。
compute_distances：计算簇之间的距离，即使不使用distance_threshold。这可以用来实现树状图的可视化，但是会带来计算和内存开销。

属性介绍：

labels_:每个样本的簇标记。
n_leaves_:分层树的叶结点数量。
n_components_:连接图中连通分量的估计值。
children_:一个数组,给出了每个非叶结点中的子节点数量。

方法介绍：

fit(XK[，y]):训练模型。
fit_predict(X[，y]):训练模型并预测每个样本所属的簇标记。

3.算法实战

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn import cluster
from sklearn.metrics import adjusted_rand_score


# make_blobs函数产生的是分隔的高斯分布的聚类簇
def create_data(centers, num=100, std=0.7):
    X, labels_true = make_blobs(n_samples=num, centers=centers, cluster_std=std)
    return X, labels_true


# 观察生成点
def plot_data(*data):
    X, labels_true = data
    labels = np.unique(labels_true)
    fig, ax = plt.subplots()
    colors = 'rgbyckm'
    for i, label in enumerate(labels):
        position = labels_true == label
        # 散点图
        ax.scatter(X[position, 0], X[position, 1], label="cluster %d" % label, color=colors[i % len(colors)])
    # 图例位置
    ax.legend(loc='best')
    ax.set_xlabel("X_0")
    ax.set_ylabel("X_1")
    ax.set_title('data')
    plt.show()


# 考察簇的数量与连接方式对聚类效果的影响
def test_AGNES(*data):
    X, label_true = data
    nums = range(1, 20)
    linkages = ['ward', 'complete', 'average']
    result = []
    for i, linkage in enumerate(linkages):
        # ARI指数
        ARIS = []
        for num in nums:
            cls = cluster.AgglomerativeClustering(n_clusters=num, linkage=linkage)
            predicted_labels = cls.fit_predict(X)
            # ARI指标
            ARIS.append(adjusted_rand_score(label_true, predicted_labels))
        result.append(ARIS)
    return nums, result


# 寻找最佳聚类中心
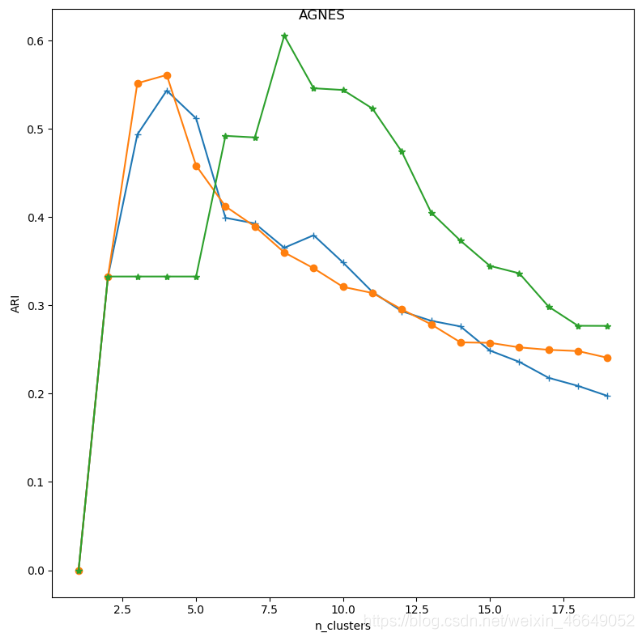
def plot_kmeans(*data):
    fig, ax = plt.subplots(1, 1, figsize=(8, 8))
    ax.plot(nums, result[0], marker="+")
    ax.plot(nums, result[1], marker="o")
    ax.plot(nums, result[2], marker="*")
    ax.set_xlabel(r"n_clusters")
    ax.set_ylabel("ARI")
    fig.suptitle("AGNES")
    plt.show()


if __name__ == '__main__':
    centers = np.asarray([[1, 1], [2, 2], [1, 2], [10, 20]])
    # 构造数据
    X, labels_true = create_data(centers, num=1000, std=0.5)
    # 观察生成点
    plot_data(X, labels_true)
    nums, result = test_AGNES(X, labels_true)
    plot_kmeans(nums, result)

在这里插入图片描述

四、总结

scikit-learn给出了一份聚类模型参数调整和使用场景的建议，这里介绍如下：
在这里插入图片描述
在实际应用中，聚类簇的数量的选取通常结合性能度量指标和具体问题分析。如给出了ARI 随n_clusters 的曲线。我们可以选择曲线上ARI最大值附近的一批n_clusters。然后具体问题具体分析:如果要求每个簇内足够纯净，则倾向于选择较大的n_clusters，即较大的簇数量(极端情况下，每个样本点就是一个簇，则可以保证每个簇都是纯净的)。如果要求尽可能地将相似的样本划归到一个簇中，则倾向于选择较小的n_clusters，即较小的簇数量(极端情况下，我们认为所有的样本点都是相似的，则都划归到一个簇中)。