本站消息

站长简介/公众号

出租广告位,需要合作请联系站长

天上飘来一个字

4086

文章

1910907

访问

+关注

分类

暂无分类

日期归档

2024-11(1)

图形学基础|屏幕空间反射(SSR)

发布于2021-09-04 23:43 阅读(1046) 评论(0) 点赞(13) 收藏(0)

图形学基础|屏幕空间反射(SSR)

文章目录

图形学基础|屏幕空间反射(SSR)

一、前言

反射效果，是游戏中比较常见且重要的一个效果。

在表现光滑的表面（金属、光滑地面）、水面（湖面、地面积水）等材质时，反射出场景中的其他物体，可以让画面质量有很大提升，丰富真实感。

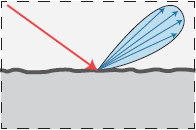
在这里插入图片描述

当粗糙度越小，镜面反射的反射波瓣更加狭窄，光照更加高频，精度要求也更高。

在这里插入图片描述

本文将对实现反射效果的一些技术做简单的概述，并着重介绍基于屏幕空间的反射技术。

以下是笔者的一些笔记。如有错误，还请见谅。

二、反射技术概述

这里所说的反射，属于间接光照的范畴。

直接光照下的反射是指：光源出发经过物体表面直接反射进入眼睛的光照。

间接光照下的反射是指：当物体的表面比较光滑（如镜面，金属），其表面可以反射周围环境，反射的光线进入人眼。

间接光照下的反射，如果严格计算求解，是相当复杂的：

需要对表面上的像素在其法线方向做半球积分；
并且光线经反射会继续地传递下去，直至能量衰减为0；

在实时渲染当中，完整地计算求解间接光照下的反射是很困难的，因此需要通过各种技术手段模拟和近似反射效果。

各种性能友好的反射方法就应运而生，其中包含了以下几种常用的技术方案：

环境贴图反射；
IBL反射；
平面反射；
屏幕空间反射；

2.1 环境贴图反射

最简单的模拟反射效果的技术方案是环境贴图反射（CubeMap反射）。

这种技术通过计算反射的向量，采样（Fetch）环境贴图，从而实现反射的效果。

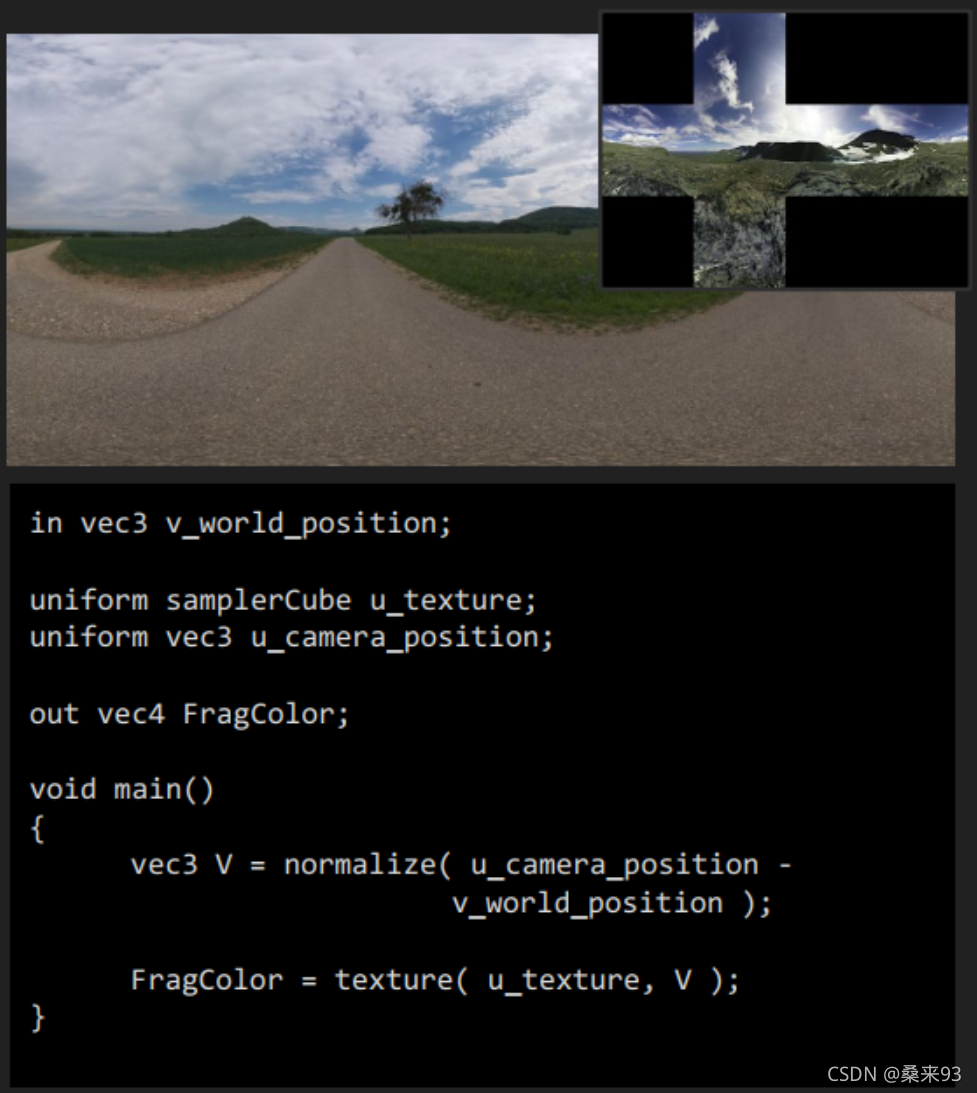
环境贴图

环境贴图CubeMap最简单的情况就是静态的环境，可以通过预先烘焙进行存储，在运行时加载渲染。

如下展示了天空盒的渲染，其中，OpenGL渲染时需要注意CubeMap的方向问题。

在这里插入图片描述

并且，环境贴图的存储方式并不局限于CubeMap（立方体），还可以是八面体映射等。

环境映射技术漫谈博文中介绍了四种环境映射技术的原理并分析了它们的优缺点。

反射向量

对环境贴图的采样需要反射向量，

计算反射向量的原理可参考图形学相关数学（反射，折射公式）。

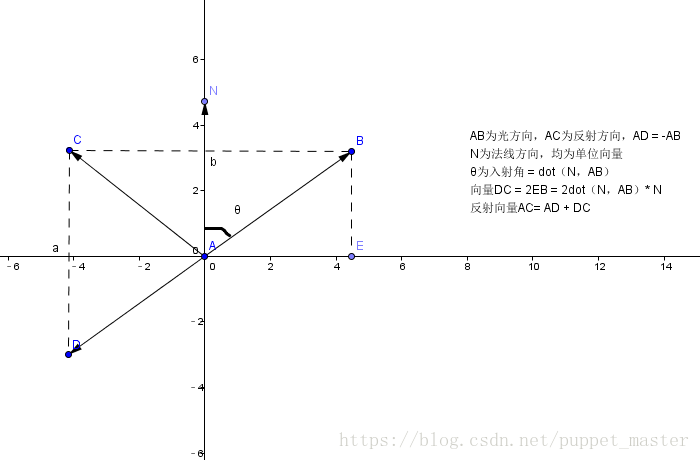
在这里插入图片描述

或在HLSL中，直接使用 reflect 函数，入射方向和法向量都为单位向量。

// 注意，V方向是指向相机的方向
// 使用reflect，需要使用反向V
float3 L = reflect(-V, N);

伪代码

模拟天空盒反射的着色器如下：

float4 PS(float2 Tex : TEXCOORD, float4 SVPosition : SV_Position) : SV_Target
{
	float3 N = normalize(v_normal);
    float3 V = normalize(v_camera_position - v_world_position);
    float3 L = reflect(-V, N);
    float3 Color = CubeMap.SampleLevel(LinearSampler, L, 0).xyz;
    return float4(Color,1.0f);
}

2.2 IBL反射

2.1的环境贴图（天空盒）反射并没有考虑到粗糙度，reflect求解的反射向量是完全镜面反射。

在PBR的IBL环境光计算中，考虑到粗糙度，根据表面的粗糙度来计算环境纹理的平均值。

因为它需要获取一个区域的所有像素，所以发射多条光线进行采样计算平均值很慢。

幸运的是，GPU可存储mipmap，mipmap是图像的模糊版本，这也适用于Cubemap。

将预预过滤环境贴图存储在Mipmap中，通过粗糙度映射计算Mipmap等级，我们就可以从立方体贴图获取一个区域的环境纹理平均值了。

实现方面可以参考笔者之前文章中的5.2.2 Prefilter EnvironmentMap。

在这里插入图片描述

在实际应用时，会在场景中放置多个Reflection Probe/反射探针。

在场景中选择一些关键位置，每个Reflection Probe都以自己所在位置为中心烘焙周围的环境光照。

在渲染场景中的物体时, 选择一个或多个最近的Refelction Probe, 来确定周围的环境光照信息，尽管反射不够精确，但反射足够接近。

在这里插入图片描述

2.3 平面反射（Planar Reflections）

如果我们只关心平面上的反射，有这样一个办法。

在平面上反射的相机的角度渲染场景，将结果存储在纹理中，并在最终渲染过程中使用它。

如果是粗糙的平面，可以对得到的像再次进行模糊等后处理。

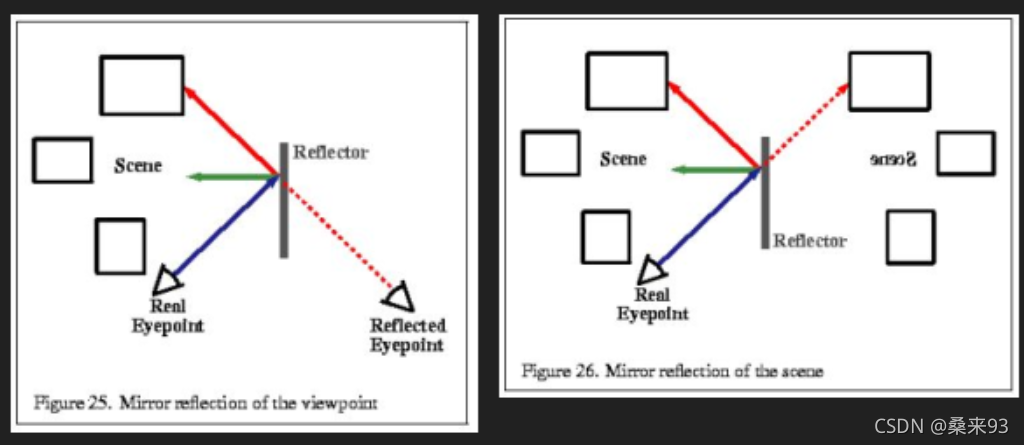
在这里插入图片描述

这是昂贵的，因为需要对反射进行整个场景的完整渲染。

可参考的实现有：

2.4 屏幕空间反射（Screen Space Reflection）

2.4.1 SSR的基本原理

屏幕空间反射（Screen Space Reflection，SSR），是一个非常著名的基于屏幕空间的技术。

由于镜面反射的波瓣很窄，意味着可以使用少量的光线模拟反射，从而就可以得到不错的效果。

算法本身的原理非常简单：

对于屏幕空间上的物体的每个像素，根据该像素对应的法线和视线信息，求解出反射向量；
当前点沿着反射向量在屏幕空间进行步进，判断步进后的坐标深度与深度缓存中存储的物体深度是否相交；
若相交，取交点处的物体颜色作为最终的反射颜色；

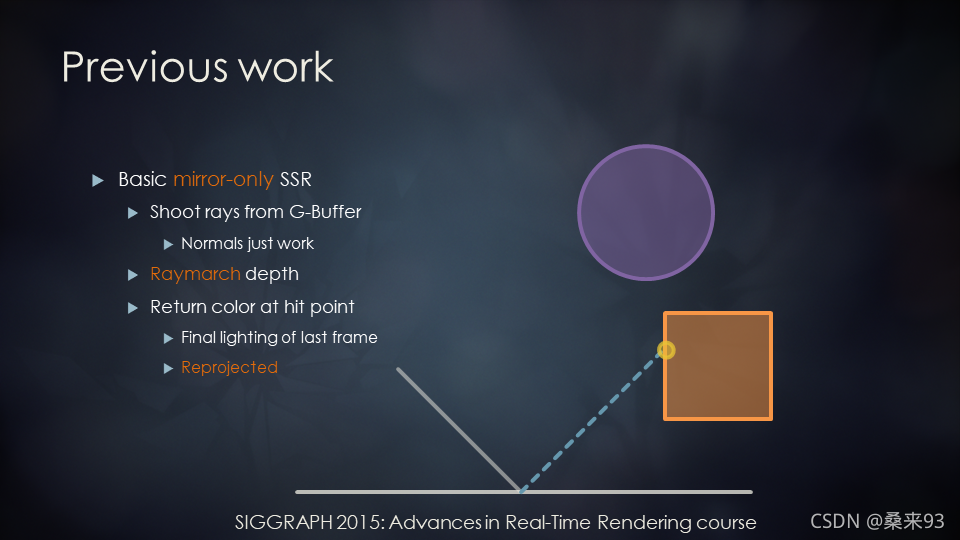
在这里插入图片描述

2.4.2 SSR的优缺点

优点：

针对任何面都可以实时反射，不需要求平面。
不需要额外的DrawCall，没有Planar Reflection那种翻倍DC的问题，计算都在GPU，解放CPU。
只需要额外的后处理Pass处理，无需大规模改动引擎管线，容易集成。
可以与Reflection Probe等结合使用。

缺点：

需要全屏深度和全屏法线，延迟渲染管线中是可以免费拿到的！但是前向渲染的话，需要额外渲染一遍DepthNormalMap。
Shader中需要进行RayMarching，对于GPU的负载较大，且步进是有一定步长的，它本身不可能非常精确。
效果存在自身缺陷，由于只有屏幕可见的物体信息，不在屏幕内的，就完全不会反射。这属于技术本身的瓶颈。

三、SSR（Screen-Space Reflection）实现

3.1 Efficient GPU Screen-Space Ray Tracing

2.4.1中介绍了屏幕空间反射的基本原理：

在屏幕空间进行光线步进（Ray Marching）代替三维空间的光线步进，通过深度缓存判断是否相交。若相交，取交点处的物体颜色作为最终的反射颜色。

3.1.1 2D Raymarching vs 3D Raymarching

问题1：为什么要用屏幕空间的光线步进代替三维空间的光线步进呢？

三维空间的光线步进过程如下（以世界空间为例）：

对于着色点 $x$ ，根据其法线和视角方向，计算得到反射方向 $R$ ；
以着色点 $x$ 为起点，沿着反射方向 $R$ ，每次步进一定距离，得到一个新的点，记作 $x_i$ ， $x_i = x + i * \Delta p$ 。
将这个新的点投影到屏幕空间，得到其UV坐标；
有了UV坐标之后，采样深度缓存，得到深度 $S a m p l e D e p t h$ ，将深度转换到世界空间与 $x_i$ 的深度进行比较。

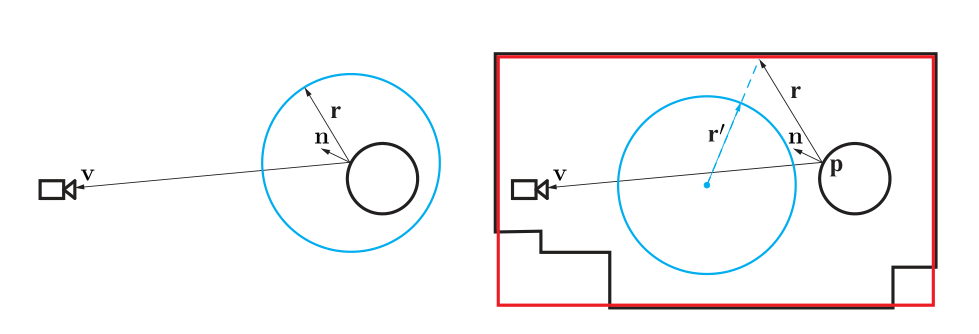
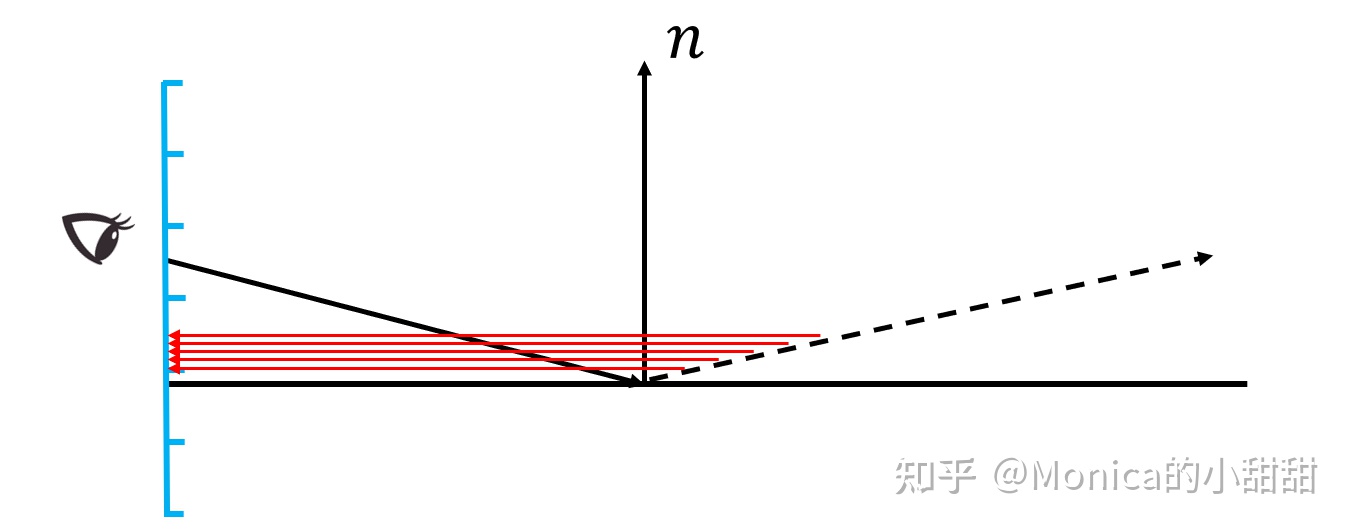
但上面的步骤存在以下的问题，如图所示。蓝色小格子代表一个一个的像素，红色代表该点所对应的像素。

可以看到，非常多的点 $x_i$ 对应的是同一个像素，这就导致了一些区域过采样。

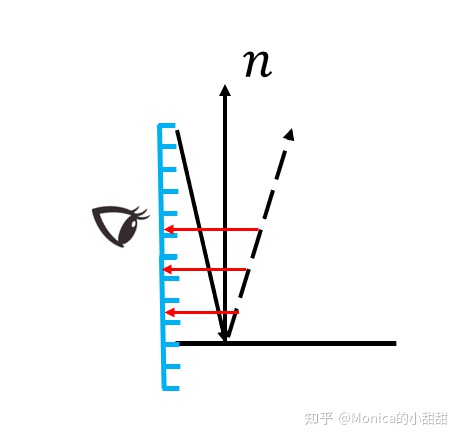
在这里插入图片描述

又有下图的情况， $x_i$ 之间的间隔又比较大（跳过了一些像素），这就导致一些区域欠采样。

在这里插入图片描述

因此，Efficient GPU Screen-Space Ray Tracing 文章提供了在屏幕空间进行光线步进的方法！

相比于基于3D空间的算法来说，有以下4点改进：

像素采样点是连续的；
每个像素采样点不会出现重复计算；
ray的取样范围会被限制在view frustum内；
算法内高效利用GPU特性，例如减少寄存器使用量、分支判断和耗时的内置函数；

问题2：如何在屏幕空间中进行光线步进？

在屏幕空间中步进，其实就是在屏幕空间画直线！

在做软光栅时，曾了解过两个经典的画直线算法，即DDA和Bresenham算法。

其中，DDA画线算法是最简单的一种画线算法，它由公式 $y = k x + b$ 推导得到。

关键之处在于如何设定单位步进，即一个方向的步进为单位步进，即1，另一个方向的步进必然是小于1。

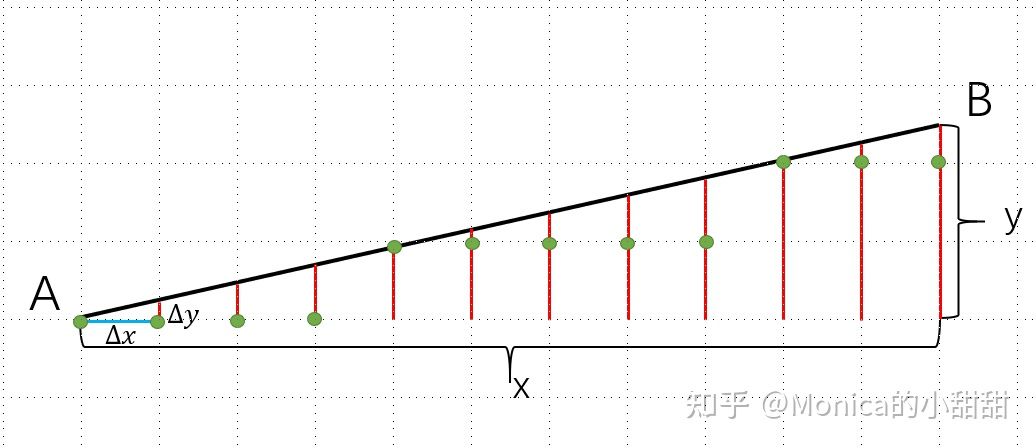
如图所示，已知点A为 $(x, y)$ ，那么下一个点 $P_0$ 为 $(x+\Delta x,y+\Delta y)$ ，再下一步则为 $P_1=P_0+(\Delta x,\Delta y)$ 。

主方向的步进单位一直为1，另一个方向的步进距离则为小于1的斜率，即：

$\left\{$

\begin{matrix} Δ x & = 1 \\ Δ y & = \frac{y_{B} - y_{A}}{x_{B} - x_{A}} \end{matrix}

$\begin{matrix} \Delta x & = 1 \\ \Delta y & = \frac{y_B-y_A}{x_B-x_A} \end{matrix}$ \right.

{Δ x Δ y = 1 = \frac{y _{B} - y _{A}}{x _{B} - x _{A}}

在这里插入图片描述

通过DDA算法，可以得到直线结果：

在这里插入图片描述

伪代码如下：

// 为了代码的简洁则可以交换x和y
if(abs(xB - xA) < abs(yB -yA))
    swap(A,B);
float deltaX = 1.0f;
float deltaY = (yB - yA) / (xB - xA);
Point P = A;
for A to B
    P += float2(deltaX, deltaY);
    DrawPixel(int(P.x),int(P.y));

通过上述DDA算法实现的屏幕空间步进，可以明显地看出其与3D空间步进的区别：

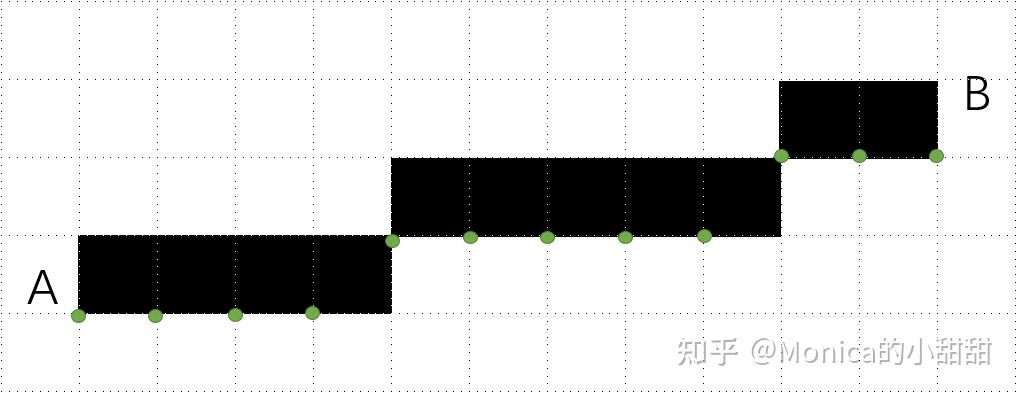
3D空间中均匀步进后的采样点坐标投射到2D屏幕空间中，点与点之间的步长却是不均匀的，会出现跳过某些屏幕区域甚至在某些点处重复计算。如下图左所示，红色点标记的为过采样区域。
屏幕空间的步进可以保证：像素采样点是连续的，并且每个像素采样点不会出现重复计算。如下图右所示。

在这里插入图片描述

3.1.2 实现

论文的文章同样提供了示例的Shader代码，同时参考UE4实现屏幕空间反射的着色器代码SSRTRelections.usf。

屏幕空间步进起点和方向

float3 Screen0 = float3(Tex, Depth);
// 恢复世界坐标
float3 World0 = UnprojectScreen(Screen0);
float3 V = normalize(CameraPos - World0);
// 反射方向
float3 L = reflect(-V, N);

float3 World1 = World0 + L * WorldThickness;
float3 Screen1 = ProjectWorldPos(World1);

// 步进起点
float3 StartScreen = Screen0;
// 步进方向
float3 StepScreen = normalize(Screen1 - Screen0);

步进与相交测试

for (int i = 0; i < MaxLinearStep; ++i)
{
    // 光线步进
    Ray += Step;
    // 到达边界，没有相交
    if (Ray.z < 0 || Ray.z > 1)
        return false;
    // 采样深度
    Depth = SceneDepthZ.SampleLevel(PointSampler, Ray.xy, 0).x;
    // 相交测试
    if (Depth + PerPixelCompareBias < Ray.z && Ray.z < Depth + PerPixelThickness)
    {
        // 返回相交的UV和深度
        OutHitUVz = Ray;
        return true;
    }
}

如何判断是否相交（笔者这里采用的是0到1的深度，即越靠近相机深度值越小）。

笔者这里为：

只有当光线步进的深度 $R a y . z$ 大于采样得到的深度 $D e p t h$ +一个偏移，且 $R a y . z$ 小于深度 $D e p t h$ +像素厚度，才为相交测试，即击中。
PerPixelCompareBias和PerPixelThickness需要通过参数进行调节。

采样纹理

当相交测试成功，即找到反射交点。接下来就需要去取相交点的物体颜色作为最终的反射颜色。

这里我们需要去采样历史帧的颜色缓冲，涉及到时间抗锯齿中介绍到的Motion Vector Buffer，通过速度缓存，我们可以计算得到当前帧UV在上一帧的UV，进而去采样历史帧颜色缓冲。

镜面反射结果

在这里插入图片描述

粗糙度模拟

上面实现的完全是镜面反射，粗糙度为0，得到的结果并不好，一般要加入粗糙度的影响。

采用了UE4中的重要性采样方法生成反射方向。

// UE4 Random.ush
// 3D random number generator inspired by PCGs (permuted congruential generator).
uint3 Rand3DPCG16(int3 p)
{
	uint3 v = uint3(p);
	v = v * 1664525u + 1013904223u;

	// That gives a simple mad per round.
	v.x += v.y*v.z;
	v.y += v.z*v.x;
	v.z += v.x*v.y;
	v.x += v.y*v.z;
	v.y += v.z*v.x;
	v.z += v.x*v.y;

	// only top 16 bits are well shuffled
	return v >> 16u;
}

// 圆盘采样
float2 UniformSampleDisk(float2 E)
{
	float Theta = 2 * PI * E.x;
	float Radius = sqrt(E.y);
	return Radius * float2(cos(Theta), sin(Theta));
}

// [ Heitz 2018, "Sampling the GGX Distribution of Visible Normals" ]
float4 ImportanceSampleVisibleGGX( float2 DiskE, float a2, float3 V )
{
	// TODO float2 alpha for anisotropic
	float a = sqrt(a2);

	// stretch
	float3 Vh = normalize( float3( a * V.xy, V.z ) );

	// Orthonormal basis
	// Tangent0 is orthogonal to N.
	#if 1 // Stable tangent basis based on V.
		float3 Tangent0 = (V.z < 0.9999) ? normalize( cross( float3(0, 0, 1), V ) ) : float3(1, 0, 0);
		float3 Tangent1 = normalize(cross( Vh, Tangent0 ));
	#else
		float3 Tangent0 = (Vh.z < 0.9999) ? normalize( cross( float3(0, 0, 1), Vh ) ) : float3(1, 0, 0);
		float3 Tangent1 = cross( Vh, Tangent0 );
	#endif

	float2 p = DiskE;
	float s = 0.5 + 0.5 * Vh.z;
	p.y = (1 - s) * sqrt( 1 - p.x * p.x ) + s * p.y;

	float3 H;
	H  = p.x * Tangent0;
	H += p.y * Tangent1;
	H += sqrt( saturate( 1 - dot( p, p ) ) ) * Vh;

	// unstretch
	H = normalize( float3( a * H.xy, max(0.0, H.z) ) );

	float NoV = V.z;
	float NoH = H.z;
	float VoH = dot(V, H);

	float d = (NoH * a2 - NoH) * NoH + 1;
	float D = a2 / (PI*d*d);

	float G_SmithV = 2 * NoV / (NoV + sqrt(NoV * (NoV - NoV * a2) + a2));

	float PDF = G_SmithV * VoH * D / NoV;

	return float4(H, PDF);
}

// 
uint2 PixelPos = (uint2)SVPosition.xy;
uint2 Random = Rand3DPCG16(int3(PixelPos, FrameIndexMod8)).xy;

float2 E = Hammersley16(i, NumRays, Random);
float3 H = mul(ImportanceSampleVisibleGGX(UniformSampleDisk(E), a2, TangentV).xyz, TangentBasis);
float3 L = 2 * dot(V, H) * H - V;

调整粗糙度为0.1，可以得到结果如下：

在这里插入图片描述

3.2 Hi-Z Screen-Space Reflections

GPU PRO5《Hi-Z Screen-Space Cone-Traced Reflections》介绍了一种计算动态3D场景反射的新方法，适用于任意形状（不仅是平面） 的表面。

包含的技术有：

Hierarchical-Z（Hi-Z） 加速光追；
光泽反射所需的所有预计算通道。
屏幕空间椎体跟踪的技术，用于近似粗糙表面，从而产生模糊的反射。

其中，Hi-Z（层级Z）屏幕空间追跟踪算法可以通过快速收敛来反射整个场景，并且比基于线性步长的Raymarching算法快几个数量级。

接下来，将对Hi-Z的追踪算法进行介绍与实现。

3.2.1 Hi-Z Trace算法

问题1：什么是层级Z（Hierarchical-Z）？

Hierarchical-Z缓冲区，也称为Hi-Z缓冲区，是通过获取Z-buffer中四个相邻值得最小值或最大值，将其存储在原有缓冲区一半大小的缓冲区来构造的。

Hi-Z结构的最小值版本是如何运行的，如下图所示：

在这里插入图片描述

我们都知道，深度可以认为是场景几何结构的一种表示。

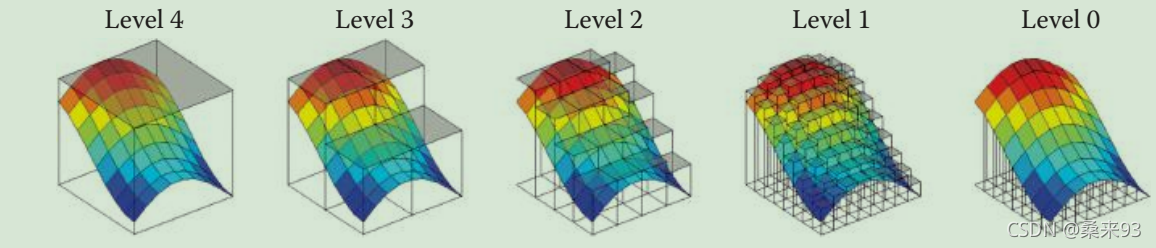
如下图，这是将Hi-Z各级缓冲反投影到世界空间的可视化结果。

可以看出当Hiz的层级越高，就表示这是对场景越粗略的近似。

在这里插入图片描述

GPU PRO5 提供了Hi-Z Buffer创建相应的Shader代码：

float4 main ( PS_INPUT input ) : SV_Target
{
    // Texture/image coord inates to sample/ load / read the depth
    // values with .
    float2 texcoords = input.tex ;
    
    float4 minDepth ;
    minDepth.x = depthBuffer . SampleLevel ( pointSampler ,    texcoords , prevLevel , int2 ( 0 , 0) ) ;
    minDepth.y = depthBuffer . SampleLevel ( pointSampler ,    texcoords , prevLevel , int2 ( 0, −1) ) ;
    minDepth.z = depthBuffer . SampleLevel ( pointSampler ,    texcoords , prevLevel , int2 ( −1, 0) ) ;
    minDepth.w = depthBuffer . SampleLevel ( pointSampler ,    texcoords , prevLevel , int2 ( −1 , −1) ) ;

    // Take th e minimum o f th e f o u r d epth v a l u e s and r e t u r n i t .
    float d = min ( min ( minDepth . x , minDepth . y ) , min ( minDepth . z ,minDepth . w ) );
    return d ;
}

问题2：如何在Hi-Z上做追踪？

在这里使用 Stochastic Screen Space Reflections 的PPT进行介绍。

Hi-Z Trace的主要思想是：通过粗略的深度来加速步进步长，在Hi-Z层级之间行进，从而快速收敛到相交点。

通过以下这个例子可以比较好地理解Hi-Z上如何进行追踪。

我们从层次结构中最精细的级别开始。

如下图，在最精细的级别，但没有相交，所以会移动到更粗糙的一层。

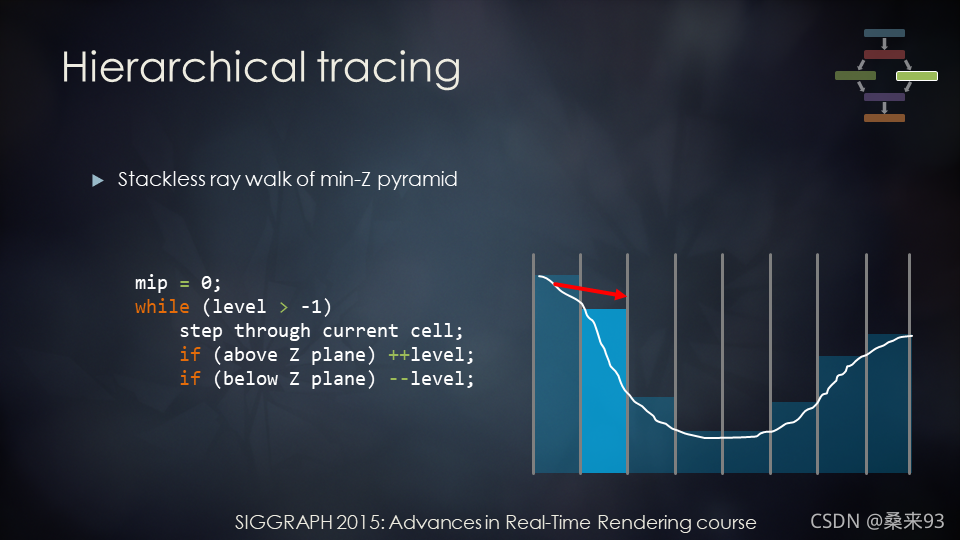
在这里插入图片描述

如下图，因为上面没有相交，所以到了粗糙的一层。因而跳过了许多空白的空间。

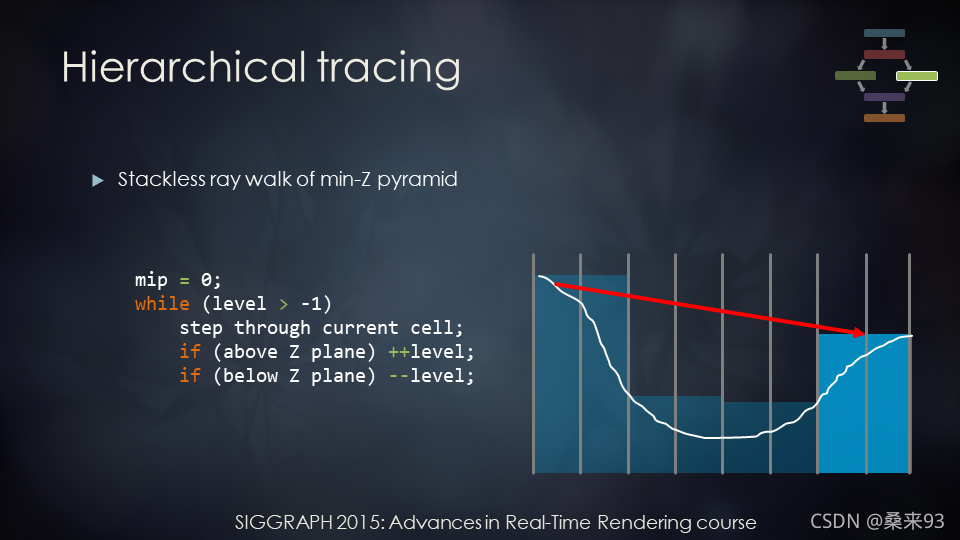
在这里插入图片描述

如下图，因为上面还是没有相交，就会进入下一层。一旦我们找到与 Z 平面的交点，我们就会移动到层次结构中更精细的级别。在这里，我们发生了相交。

在这里插入图片描述

因为发生了相交，所以要进入更精细的级别，如下图。

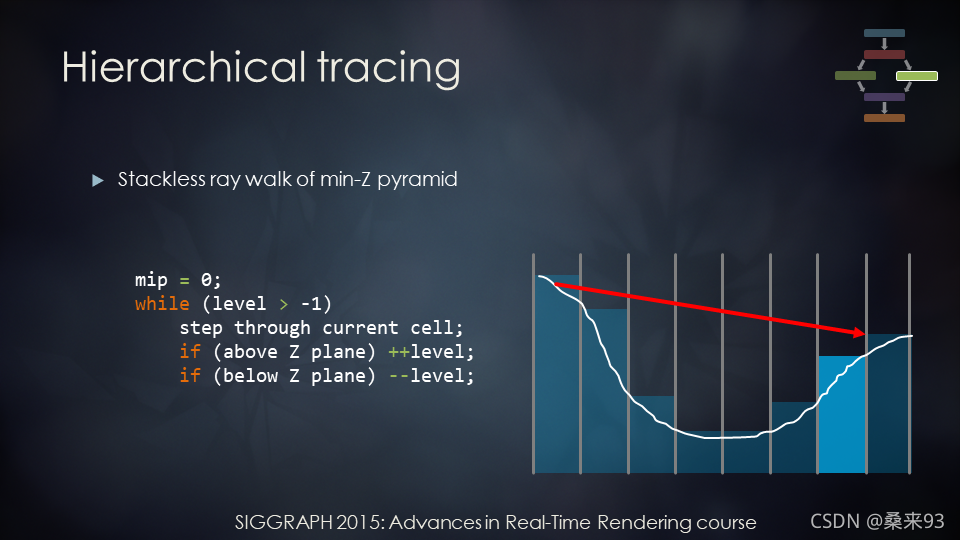
在这里插入图片描述

继续步进，一旦我们在最精确的层级相交，我们就找到了交点。

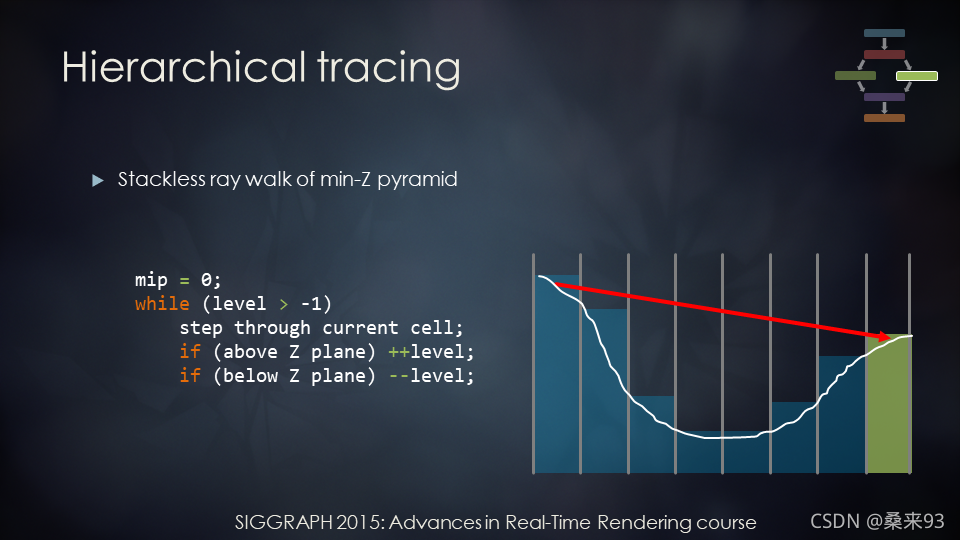
在这里插入图片描述

不像3.1中介绍的使用固定的小步长，Hi-Z通过采用大步长并通过在层次结构级别中索引来达到快速收敛。

注：

HiZ要求Buffer是严格的aligned quad tree（对齐四叉树），这样才能用于加速Raymarching的算法。
通过在不同层次结构级别中索引来有效且快速地到达我们所期望的交点/坐标。

GPU PRO5 提供了HiZTrace相应的Shader代码：

// starting level to traverse from 
// 从Level=0开始
level = 0 

// ray-trace until we descend below the root level defined by N,demo use 2
// 光线跟踪直到我们下降到由N定义的级别以下
// 层级不低于N，N以下就是一个可以认为相交的层级？
while level not below N

    minimumPlane = getCellMinimumDepthPlane(...)
    
    // reads from the Hi-Z texture using our ray
    // 使用我们的光线读取Hi-Z纹理
    boundaryPlane = getCellBoundaryDepthPlane(...)

    // gets the distance to next Hi-Z cell boundary int ray direction
    // 获取到下一个 Hi-Z 单元边界的距离 int ray 方向
    closestPlane = min(minimumPlane, boundaryPlane)
    // gets closest of both planes
    // 获得两个平面最近的那个

    ray = intersectPlane(...)
    // intersects the closest plane, returns O + D * t only.
    // 与最近的平面相交，仅返回 O + D * t。

    if intersectedMinimumDepthPlane
        // if we intersected the minimum plane we should go down a level and continue
        // 如果我们与最小平面相交，我们应该下一层并继续
        descend a level
    
    if intersectedBoundaryDepthPlane
        // if we intersected the boundary plane we should go up a level and continue
        // 如果我们与边界平面相交，我们应该向上一层并继续
        ascend a level

// we are now done with the Hi-Z ray marching so get color from the intersection
// 我们现在完成了 Hi-Z 射线行进，因此从交叉点获取颜色
color = getReflection(ray）

3.2.2 实现

Hi-Z Buffer的创建

正如3.2.1提到的：HiZ要求Buffer是严格的aligned quad tree（对齐四叉树），即缓冲的分辨率（宽、高）需要为2的幂次方。

那么HiZ的Level0（第零级）的纹理分辨率需要如何根据深度图的纹理分辨率变换得到呢？

UE4实现的方式如下：

将原图的分辨率（深度图）向上扩充成为2的幂次方；
再对宽、高分别取1/2；

例如：width = 1000，先补成1024，再取半分辨率。则为512。

计算的代码如下：

int32_t NumMipsX = std::max((int32_t)std::ceil(std::log2(ScreenWidth) - 1.0), 1);
int32_t NumMipsY = std::max((int32_t)std::ceil(std::log2(ScreenHeight) - 1.0), 1);
int32_t HZBWidth = 1 << NumMipsX;
int32_t HZBHeight = 1 << NumMipsY;

至于Level1、Level2等，则是对其上一级进行取半分率即可。

这里采用ComputeShader实现HiZBuffer的创建：

void Gather4(float2 BufferUV, out float4 MinZ)
{
    // 偏移一点，点采样周围4个像素
	float2 OffsetUV = BufferUV + float2(-0.25f, -0.25f) * SrcTexelSize;
	float2 Range = InputViewportMaxBound - SrcTexelSize;
	float2 UV = min(OffsetUV, Range);
    // 取邻近4个深度
	MinZ = SceneDepthZ.GatherRed(PointSampler, UV, 0);
}

[numthreads(8, 8, 1)]
void CS_BuildHZB(uint2 GroupId : SV_GroupID,
				 uint GroupThreadIndex : SV_GroupIndex,
				 uint2 DispatchThreadId : SV_DispatchThreadID)
{
    // SrcTexelSize，（1.f / SrcWidth，1.f / SrcHeight）
    // 求出像素在上一级的UV坐标
	float2 BufferUV = (DispatchThreadId + 0.5) * SrcTexelSize * 2.0;
	float4 MinDeviceZ4;
	Gather4(BufferUV, MinDeviceZ4);
    // 取最小深度
	float MinDeviceZ = min(min(MinDeviceZ4.x, MinDeviceZ4.y), min(MinDeviceZ4.z, MinDeviceZ4.w));
	ClosestHZB[DispatchThreadId] = MinDeviceZ;
}

Hi-Z Trace

层级Z追踪的代码实现非常美妙，NOTES ON SCREEN SPACE HIZ TRACING 提供了一份代码实现。

并做了一个追踪过程的动图，展示了如何在屏幕空间进行Hi-Z追踪。

在这里插入图片描述

结合GPU PRO5提供的代码，笔者的代码如下：

float3 IntersectDepthPlane(float3 RayOrigin, float3 RayDir, float t)
{
	return RayOrigin + RayDir * t;
}

float2 GetCellCount(float2 Size, float Level)
{
	return floor(Size / (Level > 0.0 ? exp2(Level) : 1.0));
}

float2 GetCell(float2 Ray, float2 CellCount)
{
	return floor(Ray * CellCount);
}

// 不同Cell返回真
bool CrossedCellBoundary(float2 CellIdxA, float2 CellIdxB)
{
	return CellIdxA.x != CellIdxB.x || CellIdxA.y != CellIdxB.y;
}

float2 GetMinMaxDepthPlanes(float2 Ray, float Level)
{
	return HiZBuffer.SampleLevel(PointSampler, float2(Ray.x, Ray.y), Level).rg;
}

float3 IntersectCellBoundary(
	float3 RayOrigin, float3 RayDirection, 
	float2 CellIndex, float2 CellCount, 
	float2 CrossStep, float2 CrossOffset)
{
    // 步进格子
	float2 Cell = CellIndex + CrossStep;
	Cell /= CellCount;
	Cell += CrossOffset;

	float2 delta = Cell - RayOrigin.xy;
	delta /= RayDirection.xy;
    // 取最小
	float t = min(delta.x, delta.y);
    // 步进光线
	return IntersectDepthPlane(RayOrigin, RayDirection, t);
}

bool WithinThickness(float3 Ray, float MinZ, float TheThickness)
{
	return Ray.z < MinZ + TheThickness;
}

bool CastHiZRay(float3 Start, float3 Direction, float ScreenDistance, out float3 OutHitUVz)
{
	float PerPixelThickness = ScreenDistance;
	float PerPixelCompareBias = 0.85 * PerPixelThickness;

	Direction = normalize(Direction);
	
    // Level0缓冲的分辨率
	const float2 TextureSize = RootSizeMipCount.xy;
    // 最高的Level
	const float HIZ_MAX_LEVEL = RootSizeMipCount.z - 1;
    // 0.5 in original paper, smaller value generate better result
    // 一个小的偏移量
	float2 HIZ_CROSS_EPSILON = 0.05 / TextureSize; 
	
    // 起始层级
	float Level = HIZ_START_LEVEL;
    // 迭代次数
	float Iteration = 0.f;

	float2 CrossStep = sign(Direction.xy);
	float2 CrossOffset = CrossStep * HIZ_CROSS_EPSILON;
	// for negative direction, the starting point is top-left corner, 'CrossOffset' is enough to step back one cell
    // 对于负方向，CrossOffset带有负号足够可以让Ray返回一格
	CrossStep = saturate(CrossStep);

    // 找到近平面的交点O
	float3 Ray = Start;
	float3 D = Direction.xyz / Direction.z;
	float3 O = IntersectDepthPlane(Start, D, -Start.z);

	bool intersected = false;
    
    // 起止位置
	float2 RayCell = GetCell(Ray.xy, TextureSize);
	Ray =  IntersectCellBoundary(O, D, RayCell, TextureSize, CrossStep, CrossOffset);
    
	while (Level >= HIZ_STOP_LEVEL && Iteration < MAX_ITERATIONS)
	{
		const float2 CellCount = GetCellCount(TextureSize, Level);
		const float2 OldCellIdx = GetCell(Ray.xy, CellCount);
		if (Ray.z > 1.0)
			return false;
		
		float2 MinMaxZ = GetMinMaxDepthPlanes(Ray.xy, Level);
		float t = max(Ray.z, MinMaxZ.x + PerPixelCompareBias);
		float3 TempRay = IntersectDepthPlane(O, D, t);
		const float2 NewCellIdx = GetCell(TempRay.xy, CellCount);
        
        // 不同的Cell，表示没有碰撞，继续步进
		if (CrossedCellBoundary(OldCellIdx, NewCellIdx))
		{
			TempRay = IntersectCellBoundary(O, D, OldCellIdx, CellCount, CrossStep, CrossOffset);
			Level = min(HIZ_MAX_LEVEL, Level + 2);
		}
		else if (Level == HIZ_START_LEVEL && WithinThickness(TempRay, MinMaxZ.x, PerPixelThickness))
		{
            // 在Level0，且满足厚度的相交条件，则相交！
			intersected = true;
		}
		Ray = TempRay;
		--Level;
		++Iteration;
	}
	OutHitUVz = Ray;
	return intersected;
}

效果如下：

在这里插入图片描述